In what is becoming an ongoing series where I climb the convex optimization learning curve by making rookie mistakes, I tripped over yet another unexpected failure in my feasible point solver while testing a couple new inequality constraints for my monotonic splining project.

The symptom was that when I added minimum and maximum constraints, the feasible point solver began reporting failure. These failures made no sense to me, because they were actually constraining my problem very little, if at all. For example, I if I added constraints for s(x) > 0 and s(x) < 1, the solver began failing, even though my function (designed to behave as a CDF) was already meeting these constraints to within machine epsilon tolerance.

When I inspected its behavior, I discovered that my solver found a point x where the smooth-max was minimized, and reported this answer as also being the minimum possible value for the true maximum. As it happened, this value for x was positive (non-satisfying) for the true max, even though better locations did exist!

This time, my error turned out to be that I had assumed the smooth-max function is “minimum preserving.” That is, I had assumed that the minimum of smooth-max is the same as the corresponding minimum for the true maximum. I cooked up a quick jupyter notebook to see if I could prove I was wrong about this, and sure enough came up with a simple visual counter-example:

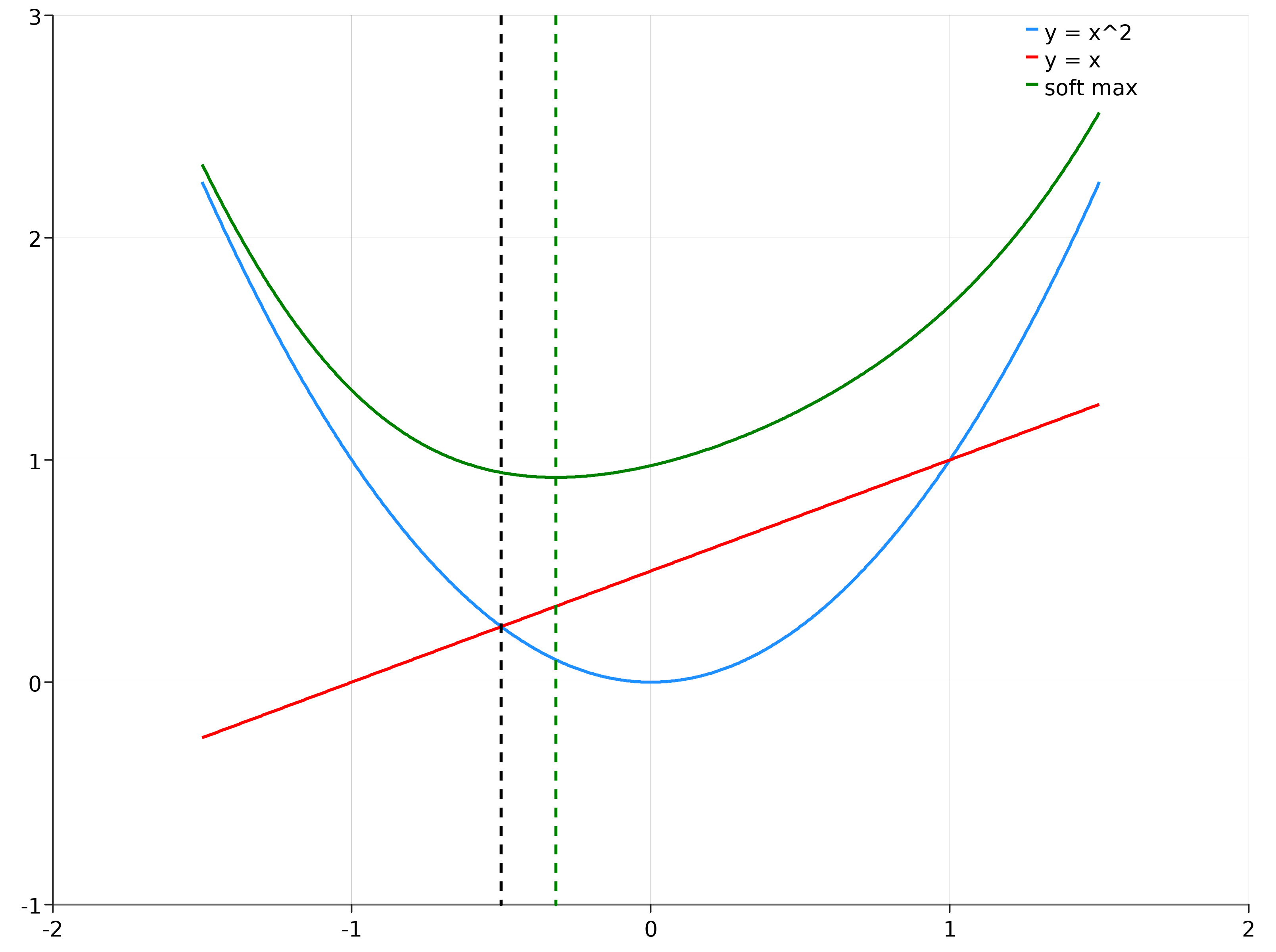
Figure-1

In this plot, the black dotted line identifies the minimum of the true maximum: the left intersection of the blue parabola and red line. The green dotted line shows the mimimum of soft-max, and it’s easy to see that they are completely different!

I haven’t yet coded up a fix for this, but my basic plan is to allow the smooth-max alpha to increase whenever it fails to find a feasible point. Why? Increasing alpha causes the smooth-max to more closely approximate true max. If the soft-max approximation becomes sufficiently close to the true maximum, and no solution is found, then I can report an empty feasible region with more confidence.

Why did I make this blunder? I suspect it is because I originally only visualized symmetric examples in my mind, where the mimimum of smooth-max and true maximum is the same. Visual intuitions are only as good as your imagination!