Equality Constraints for Cubic B-Splines
In my previous post
I derived the standard-form polynomial coefficients for cubic B-splines.
As part of the same project,
I also need to add a feature that allows the library user to declare equality constraints of the form
I expected this to be tricky, but it turns out I did most of the work already.
I can take one of my previously-derived expressions for S(x) and put it into a form that gives me coefficients for the four contributing knot points
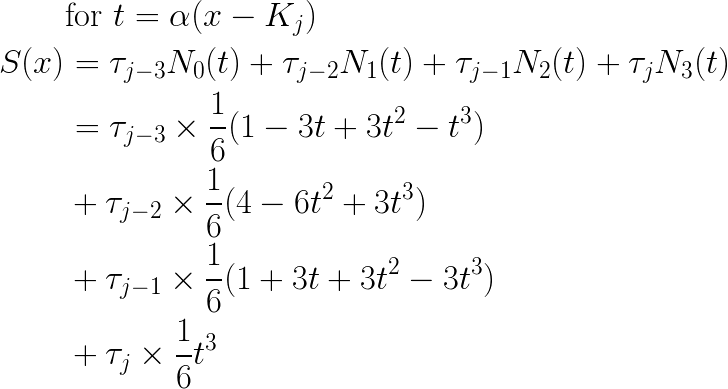
Recall that by the convention from my previous post,
My linear constraint equation is with respect to the vector I am solving for, in particular vector (τ), and so the equation above yields the following:
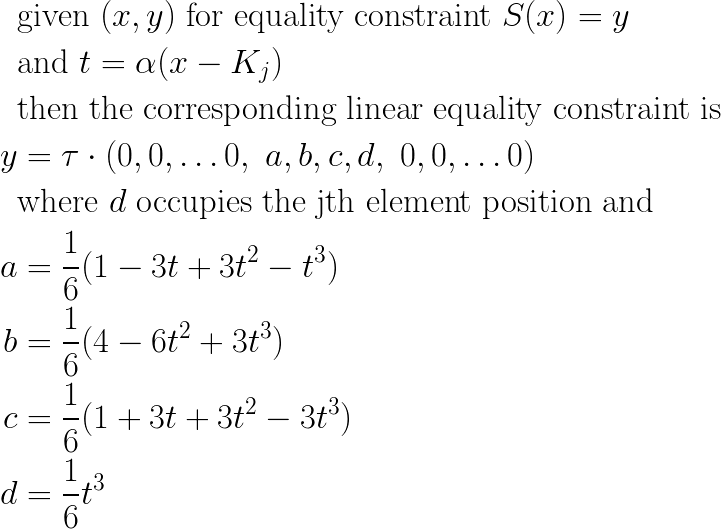
In this form, it is easy to add into a convex optimization problem as a linear equality constraint.
Gradient constraints are another common equality constraint in convex optimization, and so I can apply very similar logic to get coefficient values corresponding to the gradient of S:
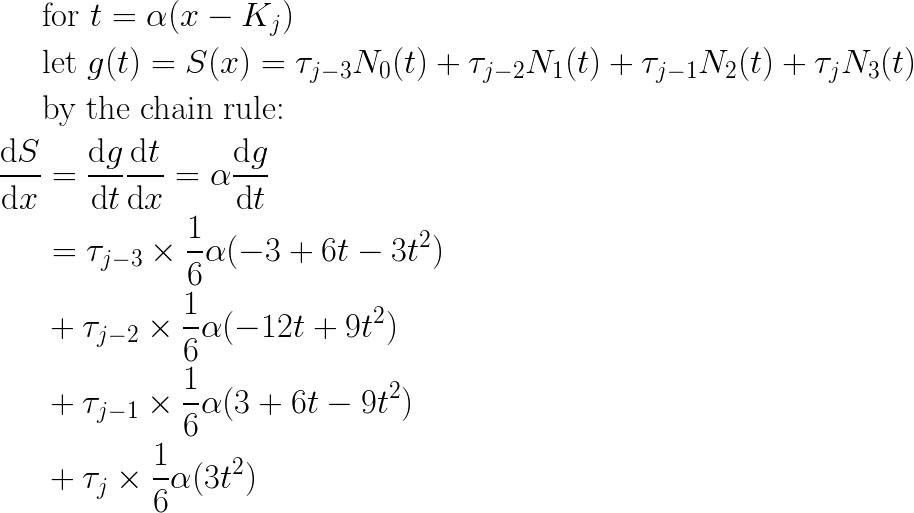
And so my linear equality constraint with respect to (τ) in this case is:
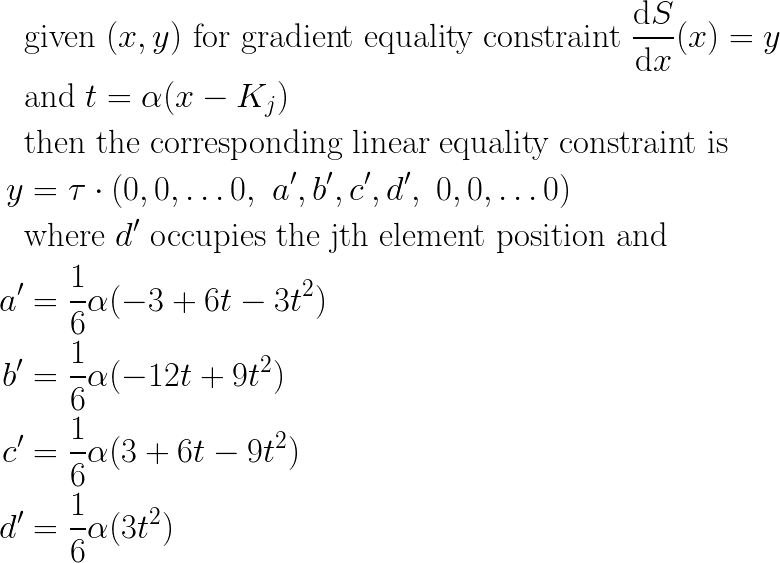
And that gives me the tools I need to let my users supply additional equality constraints as simple