Putting Cubic B-Splines into Standard Polynomial Form

Lately I have been working on an implementation of monotone smoothing splines, based on [1]. As the title suggests, this technique is based on a univariate cubic B-spline. The form of the spline function used in the paper is as follows:

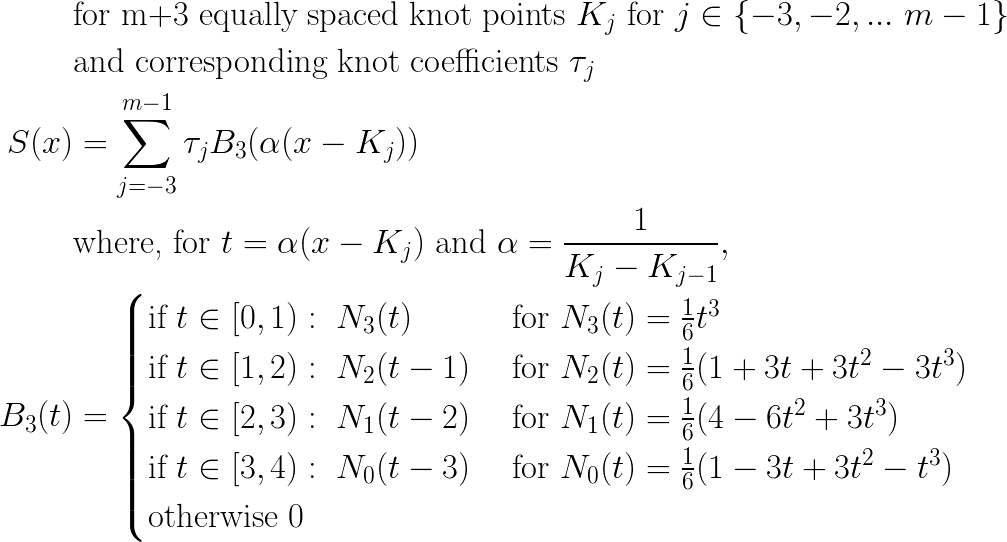
The knot points K_j are all equally spaced by 1/α, and so α normalizes knot intervals to 1. The function B₃(t) and the four N_i(t) are defined in this transformed space, t, of unit-separated knots.

I’m interested in providing an interpolated splines using the Apache Commons Math API, in particular the PolynomialSplineFunction class. In principle the above is clearly such a polynomial, but there are a few hitches.

1. PolynomialSplineFunction wants its knot intervals in closed standard polynomial form ax³ + bx² + cx + d
2. It wants each such polynomial expressed in the translated space (x-K_j), where K_j is the greatest knot point that is <= x.
3. The actual domain of S(x) is K₀ ... K_m-1. The first 3 “negative” knots are there to make the summation for S(x) cleaner. PolynomialSplineFunction needs its functions to be defined purely on the actual domain.

Consider the arguments to B₃, for two adjacent knots K_j-1 and K_j, where K_j is greatest knot point that is <= x. Recalling that knot points are all equally spaced by 1/α, we have the following relationship in the transformed space t:

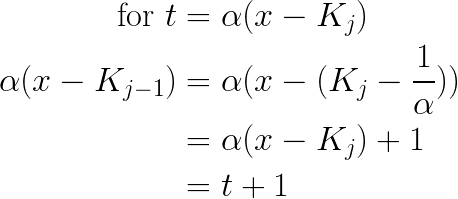
We can apply this same manipulation to show that the arguments to B₃, as centered around knot K_j, are simply {... t+2, t+1, t, t-1, t-2 ...}.

By the definition of B₃ above, you can see that B₃(t) is non-zero only for t in [0,4), and so the four corresponding knot points K_j-3 ... K_j contribute to its value:

This suggests a way to manipulate the equations into a standard form. In the transformed space t, the four nonzero terms are:

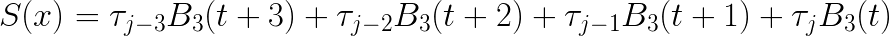
and by plugging in the appropriate N_i for each term, we arrive at:

Now, PolynomialSplineFunction is going to automatically identify the appropriate K_j and subtract it, and so I can define that transform as u = x - K_j, which gives:

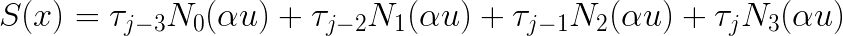
I substitute the argument (αu) into the definitions of the four N_i to obtain:

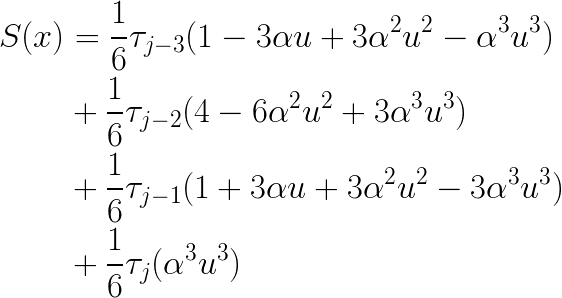
Lastly, collecting like terms gives me the standard-form coefficients that I need for PolynomialSplineFunction:

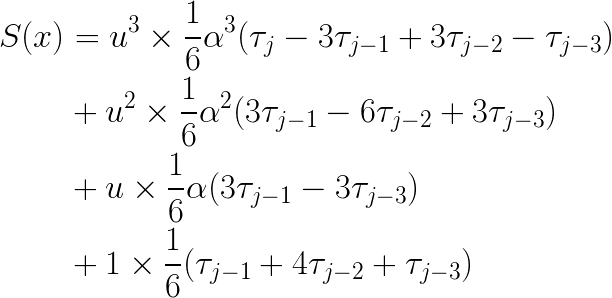
Now I am equipped to return a PolynomialSplineFunction to my users, which implements the cubic B-spline that I fit to their data. Happy computing!

References

[1] H. Fujioka and H. Kano: Monotone smoothing spline curves using normalized uniform cubic B-splines, Trans. Institute of Systems, Control and Information Engineers, Vol. 26, No. 11, pp. 389–397, 2013