In a previous post I discussed some unintuitive aspects of the distribution of distances as spatial dimension changes. To help explain this to myself I derived a formula for this distribution, assuming a unit multivariate Gaussian. For distance (aka radius) r, and spatial dimension d, the PDF of distances is:

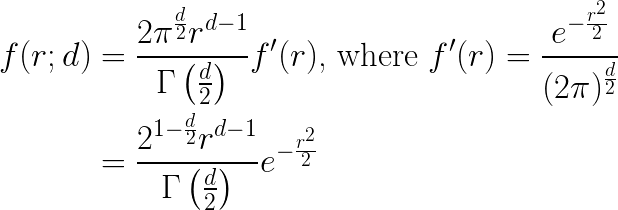
Figure 1

Recall that the form of this PDF is the generalized gamma distribution, with scale parameter a=sqrt(2), shape parameter p=2, and free shape parameter (d) representing the dimensionality.

I was interested in fitting parameters to such a distribution, using some distance data from a clustering algorithm. SciPy comes with a predefined method for fitting generalized gamma parameters, however I wished to implement something similar using Apache Commons Math, which does not have native support for fitting a generalized gamma PDF. I even went so far as to start working out some of the math needed to augment the Commons Math Automatic Differentiation libraries with Gamma function differentiation needed to numerically fit my parameters.

Meanwhile, I have been fitting a non generalized gamma distribution to the distance data, as a sort of rough cut, using a fast non-iterative approximation to the parameter optimization. Consistent with my habit of asking the obvious question last, I tried plotting this gamma approximation against distance data, to see how well it compared against the PDF that I derived.

Surprisingly (at least to me), my approximation using the gamma distribution is a very effective fit for spatial dimensionalities >= 2 :

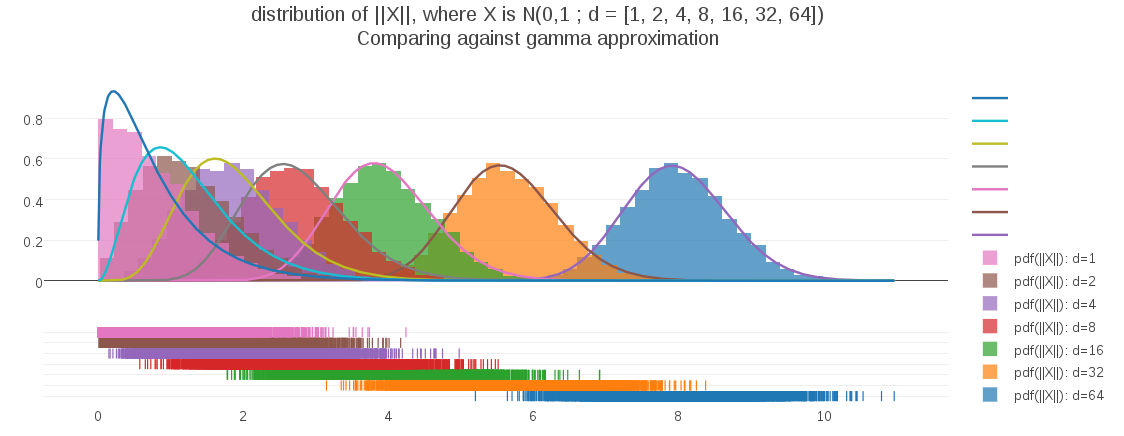
Figure 2

As the plot shows, only for the 1-dimension case is the gamma approximation substiantially deviating. In fact, the fit appears to get better as dimensionality increases. To address the 1D case, I can easily test the fit of a half-gaussian as a possible model.