Computing Derivatives of the Gamma Function

In this post I’ll describe a simple algorithm to compute the kth derivatives of the Gamma function.

I’ll start by showing a simple recursion relation for these derivatives, and then gives its derivation. The kth derivative of Gamma(x) can be computed as follows:

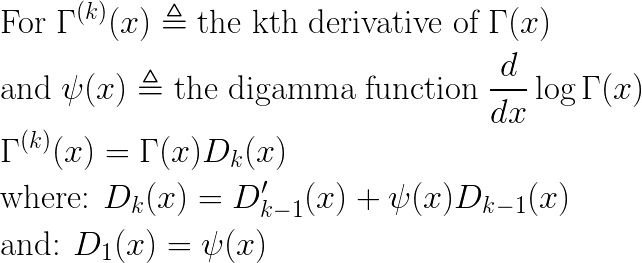
The recursive formula for the D_k functions has an easy inductive proof:

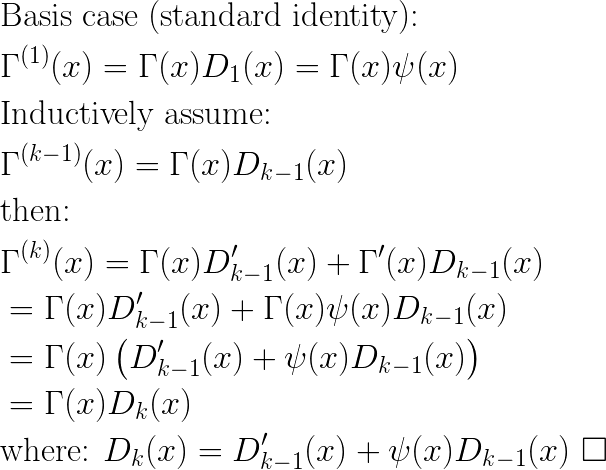
Computing the next value D_k requires knowledge of D_k-1 but also derivative D’_k-1. If we start expanding terms, we see the following:

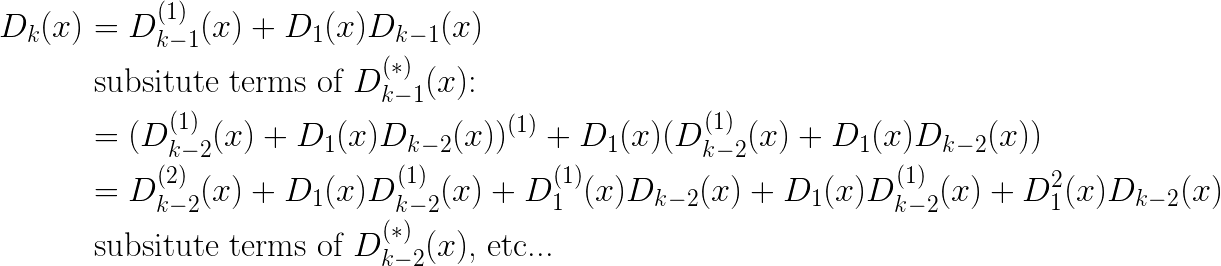
Continuing the process above it is not hard to see that we can continue expanding until we are left only with terms of D₁^(*)(x); that is, various derivatives of D₁(x). Furthermore, each layer of substitutions adds an order to the derivatives, so that we will eventually be left with terms involving the derivatives of D₁(x) up to the (k-1)th derivative. Note that these will all be successive orders of the polygamma function.

What we want, to do these computations systematically, is a formula for computing the nth derivative of a term D_k(x). Examining the first few such derivatives suggests a pattern:

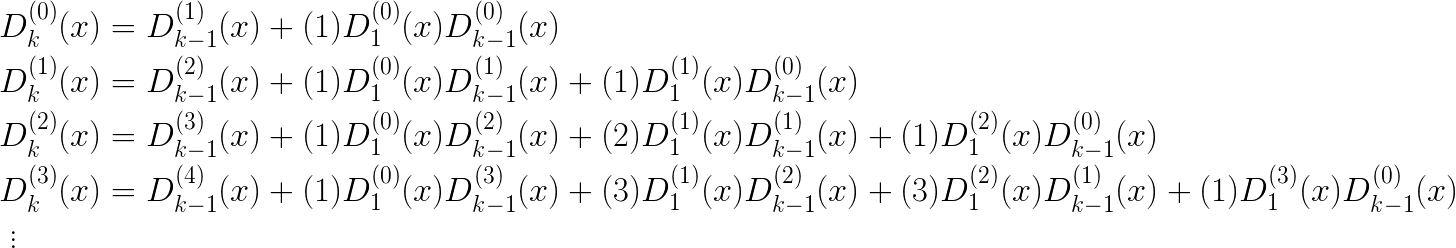
Generalizing from the above, we see that the formula for the nth derivative is:

We are now in a position to fill in the triangular table of values, culminating in the value of D_k(x):

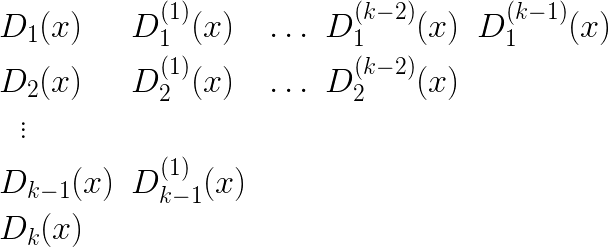
As previously mentioned, the basis row of values D₁^(*)(x) are the polygamma functions where D₁⁽ⁿ⁾(x) = polygamma⁽ⁿ⁾(x). The first two polygammas, order 0 and 1, are simply the digamma and trigamma functions, respectively, and are available with most numeric libraries. Computing the general polygamma is a project, and blog post, for another time, but the standard polynomial approximation for the digamma function can of course be differentiated… Happy Computing!