Every so often I’m reminded that the effects of changing dimensionality on objects and processes can be surprisingly counterintuitive. Recently I ran across a great example of this, while I working on a model for the distribution of distances in spaces of varying dimension.

Suppose that I draw some values from a classic one-dimensional Gaussian, with zero mean and unit variance, but that I am actually interested in their corresponding distances from center. Knowing that my Gaussian is centered on the origin, I can rephrase that as: the distribution of magnitudes of values drawn from that Gaussian. I can simulate this process by actually samping Gaussian values and taking their absolute value. When I do, I get the following result:

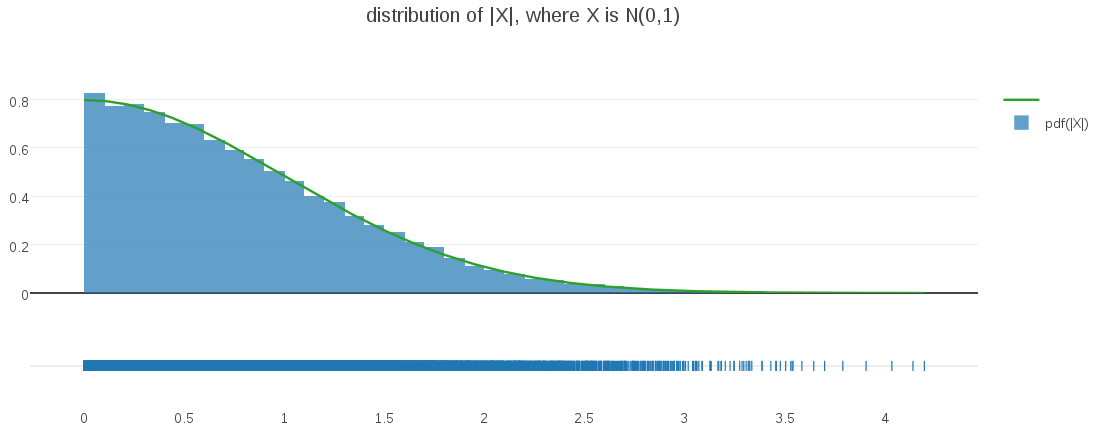
Figure 1

It’s easy to see – and intuitive – that the resulting distribution is a half-Gaussian, as I confirmed by overlaying the histogrammed samples above with a half-Gaussian PDF (displayed in green).

I wanted to generalize this basic idea into some arbitrary dimensionality, (d), where I draw d-vectors from an d-dimensional Gaussian (again, centered on the origin with unit variances). When I take the magnitudes of these sampled d-vectors, what will the probability distribution of their magnitudes look like?

My intuitive assumption was that these magnitudes would also follow a half-Gaussian distribution. After all, every multivariate Gaussian is densest at its mean, just like the univariate case I examined above. In fact I was so confident in this assumption that I built my initial modeling around it. Great confusion ensued, when I saw how poorly my models were working on my higher-dimensional data!

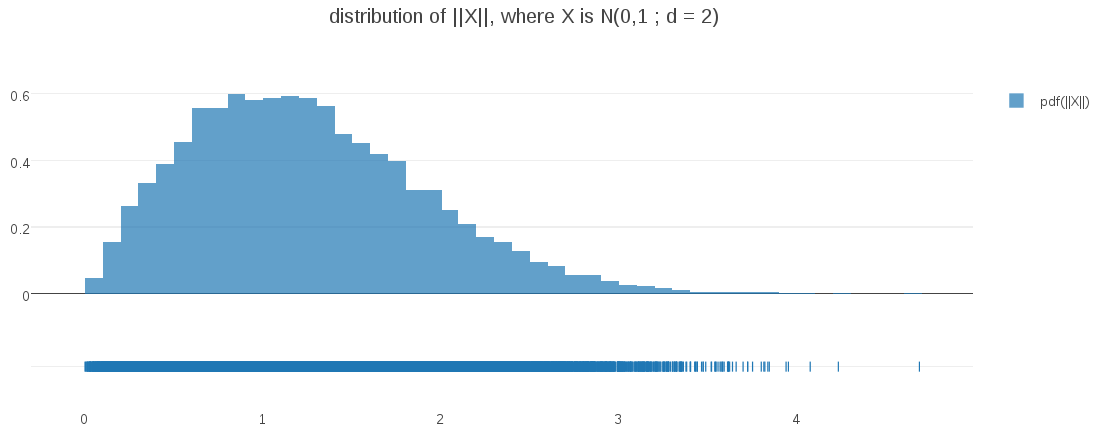
Eventually it occurred to me to do the obvious thing and generate some visualizations from higher dimensional data. For example, here is the correponding plot generated from a bivariate Gaussian (d=2):

Figure 2

Surprise – the distribution at d=2 is not even close to half-Gaussian!. My intuitions couldn’t have been more misleading!

Where did I go wrong?

I’ll start by observing what happens when I take a multi-dimensional PDF of vectors in (d) dimensions and project it down to a one-dimensional PDF of the corresponding vector magnitudes. To keep things simple, I will be assuming a multi-dimensional PDF \(f_r(\vec{x_d})\) that is (1) centered on the origin, and (2) is radially symmetric; the pdf value is the same for all points at a given distance from the origin. For example, any multivariate Gaussian with \(\vec{0_d}\) mean and \(I_d\) for a covariance matrix satisfies these two assumptions. With this in mind, you can see that the process of projecting from vectors in \(R_d\) to their distance from \(\vec{0_d}\) (their magnitude) is equivalent to summing all densities \(f_r(\vec{x_d})\) along the surface of “d-sphere” radius (r) to obtain a pdf \(f(r)\) in distance space. With assumption (2) we can simplify that integration to just \(f(r) = A_d(r)f'(r)\) , where \(f'(r)\) defines the value of \(f_r(\vec{x})\) for all \(\vec{x}\) with magnitude of (r), and \(A_d(r)\) is the surface area of a d-sphere with radius (r):

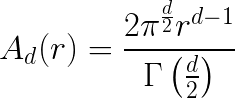
Figure 3

The key observation is that this term is a polynomial function of radius (r), with degree (d-1). When d=1, it is simply a constant multiplier and so we get the half-Gaussian distribution we expect, but when d >= 2, the term is zero at r=0, and grows with radius. Hence we see the in the d=2 plot above that the density begins at zero, then grows with radius until the decreasing gaussian density gradually drives it back toward zero again.

The above ideas can be expressed compactly as follows:

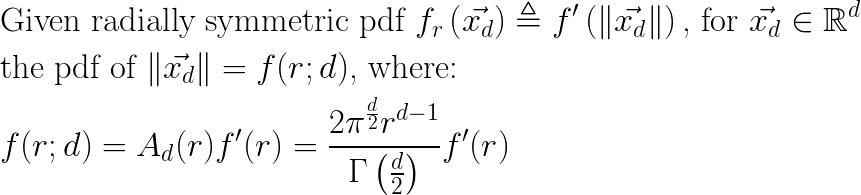
Figure 4

In my experiments, I am using multivariate Gaussians of mean \(\vec{0_d}\) and unit covariance matrix \(I_d\) , and so the form for \(f(r;d)\) becomes:

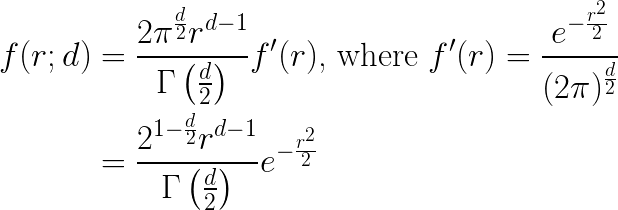
Figure 4

This form is in fact the generalized gamma distribution, with scale parameter \(a = \sqrt{2}\) , shape parameter \(p = 2\), and free shape parameter (d) representing the dimensionality in this context.

I can verify that this PDF is correct by plotting it against randomly sampled data at differing dimensions:

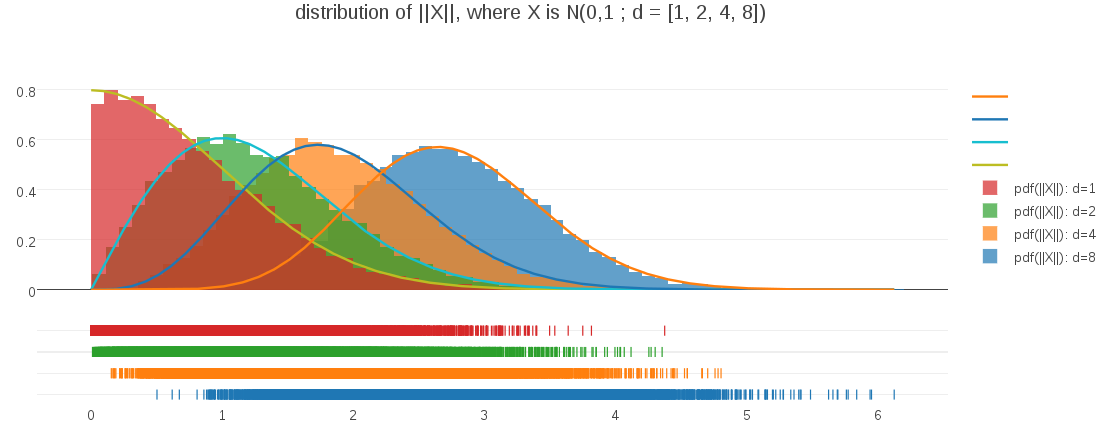
Figure 5

This plot demonstrates both that the PDF expression is correct for varying dimensionalities and also illustrates how the shape of the PDF evolves as dimensionality changes. For me, it was a great example of challenging my intuitions and learning something completely unexpected about the interplay of distances and dimension.