Efficient Multiplexing for Spark RDDs
In this post I’m going to propose a new abstract operation on Spark RDDs – multiplexing – that makes some categories of operations on RDDs both easier to program and in many cases much faster.
My main working example will be the operation of splitting a collection of data elements into N randomly-selected subsamples. This operation is quite common in machine learning, for the purpose of dividing data into a training and testing set, or the related task of creating folds for cross-validation.
Consider the current standard RDD method for accomplishing this task, randomSplit(). This method takes a collection of N weights, and returns N output RDDs, each of which contains a randomly-sampled subset of the input, proportional to the corresponding weight. The randomSplit() method generates the jth output by running a random number generator (RNG) for each input data element and accepting all elements which are in the corresponding jth (normalized) weight range. As a diagram, the process looks like this at each RDD partition:

The observation I want to draw attention to is that to produce the N output RDDs, it has to run a random sampling over every element in the input for each output. So if you are splitting into 10 outputs (e.g. for a 10-fold cross-validation), you are re-sampling your input 10 times, the only difference being that each output is created using a different acceptance range for the RNG output.
To see what this looks like in code, consider a simplified version of random splitting that just takes an integer n and always produces (n) equally-weighted outputs:
def splitSample[T :ClassTag](rdd: RDD[T], n: Int, seed: Long = 42): Seq[RDD[T]] = {
Vector.tabulate(n) { j =>
rdd.mapPartitions { data =>
scala.util.Random.setSeed(seed)
data.filter { unused => scala.util.Random.nextInt(n) == j }
}
}
}
(Note that for this method to operate correctly, the RNG seed must be set to the same value each time, or the data will not be correctly partitioned)
While this approach to random splitting works fine, resampling the same data N times is somewhat wasteful. However, it is possible to re-organize the computation so that the input data is sampled only once. The idea is to run the RNG once per data element, and save the element into a randomly-chosen collection. To make this work in the RDD compute model, all N output collections reside in a single row of an intermediate RDD – a “manifold” RDD. Each output RDD then takes its data from the corresponding collection in the manifold RDD, as in this diagram:
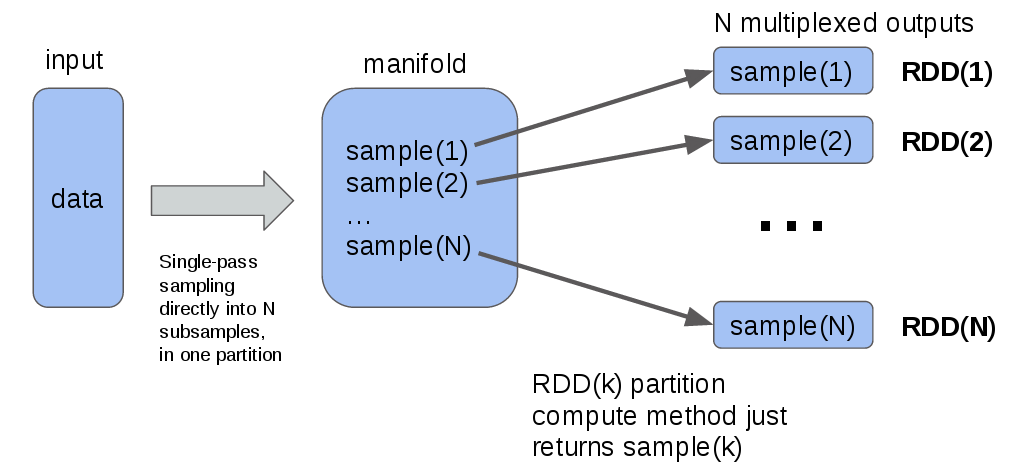
If you abstract the diagram above into a generalized operation, you end up with methods that might like the following:
def muxPartitions[U :ClassTag](n: Int, f: (Int, Iterator[T]) => Seq[U],
persist: StorageLevel): Seq[RDD[U]] = {
val mux = self.mapPartitionsWithIndex { case (id, itr) =>
Iterator.single(f(id, itr))
}.persist(persist)
Vector.tabulate(n) { j => mux.mapPartitions { itr => Iterator.single(itr.next()(j)) } }
}
def flatMuxPartitions[U :ClassTag](n: Int, f: (Int, Iterator[T]) => Seq[TraversableOnce[U]],
persist: StorageLevel): Seq[RDD[U]] = {
val mux = self.mapPartitionsWithIndex { case (id, itr) =>
Iterator.single(f(id, itr))
}.persist(persist)
Vector.tabulate(n) { j => mux.mapPartitions { itr => itr.next()(j).toIterator } }
}
Here, the operation of sampling is generalized to any user-supplied function that maps RDD partition data into a sequence of objects that are computed in a single pass, and then multiplexed to the final user-visible outputs. Note that these functions take a StorageLevel argument that can be used to control the caching level of the internal “manifold” RDD. This typically defaults to MEMORY_ONLY, so that the computation can be saved and re-used for efficiency.
An efficient split-sampling method based on multiplexing, as described above, might be written using flatMuxPartitions as follows:
def splitSampleMux[T :ClassTag](rdd: RDD[T], n: Int,
persist: StorageLevel = MEMORY_ONLY,
seed: Long = 42): Seq[RDD[T]] =
rdd.flatMuxPartitions(n, (id: Int, data: Iterator[T]) => {
scala.util.Random.setSeed(id.toLong * seed)
val samples = Vector.fill(n) { scala.collection.mutable.ArrayBuffer.empty[T] }
data.foreach { e => samples(scala.util.Random.nextInt(n)) += e }
samples
}, persist)
To test whether multiplexed RDDs actually improve compute efficiency, I collected run-time data at various split values of n (from 1 to 10), for both the non-multiplexing logic (equivalent to the standard randomSplit) and the multiplexed version:
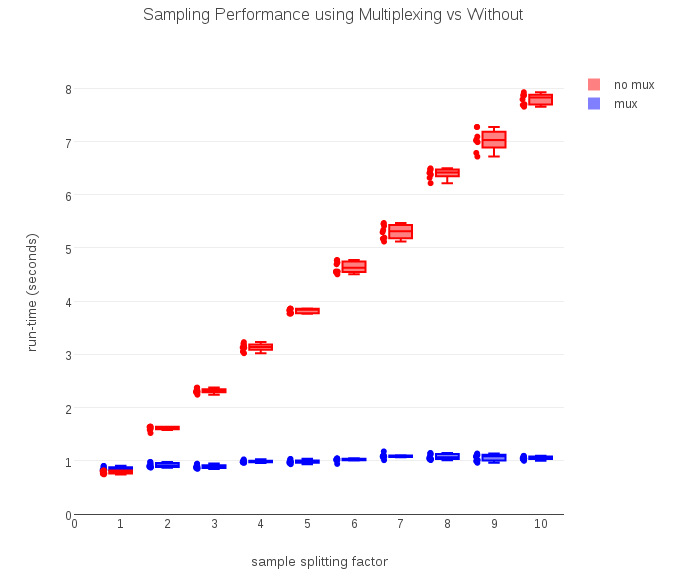
As the timing data above show, the computation required to run a non-multiplexed version grows linearly with n, just as predicted. The multiplexed version, by computing the (n) outputs in a single pass, takes a nearly constant amount of time regardless of how many samples the input is split into.
There are other potential applications for multiplexed RDDs. Consider the following tuple-based versions of multiplexing:
def muxPartitions[U1 :ClassTag, U2 :ClassTag](f: (Int, Iterator[T]) => (U1, U2),
persist: StorageLevel): (RDD[U1], RDD[U2]) = {
val mux = self.mapPartitionsWithIndex { case (id, itr) =>
Iterator.single(f(id, itr))
}.persist(persist)
val mux1 = mux.mapPartitions(itr => Iterator.single(itr.next._1))
val mux2 = mux.mapPartitions(itr => Iterator.single(itr.next._2))
(mux1, mux2)
}
def flatMuxPartitions[U1 :ClassTag, U2 :ClassTag](f: (Int, Iterator[T]) => (TraversableOnce[U1], TraversableOnce[U2]),
persist: StorageLevel): (RDD[U1], RDD[U2]) = {
val mux = self.mapPartitionsWithIndex { case (id, itr) =>
Iterator.single(f(id, itr))
}.persist(persist)
val mux1 = mux.mapPartitions(itr => itr.next._1.toIterator)
val mux2 = mux.mapPartitions(itr => itr.next._2.toIterator)
(mux1, mux2)
}
Suppose you wanted to run an input-validation filter on some data, sending the data that pass validation into one RDD, and data that failed into a second RDD, paired with information about the error that occurred. Data validation is a potentially expensive operation. With multiplexing, you can easily write the filter to operate in a single efficient pass to obtain both the valid stream and the stream of error-data:
def validate[T :ClassTag](rdd: RDD[T], validator: T => Boolean) = {
rdd.flatMuxPartitions((id: Int, data: Iterator[T]) => {
val valid = scala.collection.mutable.ArrayBuffer.empty[T]
val bad = scala.collection.mutable.ArrayBuffer.empty[(T, Exception)]
data.foreach { e =>
try {
if (!validator(e)) throw new Exception("returned false")
valid += e
} catch {
case err: Exception => bad += (e, err)
}
}
(valid, bad)
})
}
RDD multiplexing is currently a PR against the silex project. The code I used to run the timing experiments above is saved for posterity here.
Happy multiplexing!