A Library of Binary Tree Algorithms as Mixable Scala Traits

In this post I am going to describe some work I’ve done recently on a system of Scala traits that support tree-based collection algorithms prefix-sum, nearest key query and value increment in a mixable format, all backed by Red-Black balanced tree logic, which is also a fully inheritable trait.

(update) Since I wrote this post, the code has evolved into a library on the isarn project. The original source files, containing the exact code fragments discussed in the remainder of this post, are preserved for posterity here.

This post eventually became a bit more sprawling and “tl/dr” than I was expecting, so by way of apology, here is a table of contents with links:

1. Motivating Use Case
2. Library Overview
3. A Red-Black Tree Base Class
4. Node Inheritance Example: NodeMap[K,V]
5. Collection Trait Example: OrderedMapLike[K,V,IN,M]
6. Collection Example: OrderedMap[K,V]
7. Finale: Trait Mixing

A Motivating Use Case

The skeptical programmer may be wondering what the point of Yet Another Map Collection really is, much less an entire class hierarchy. The use case that inspired this work was my project of implementing the t-digest algorithm. Discussion of t-digest is beyond the scope of this post, but suffice it to say that constructing a t-digest requires the maintenance of a collection of “cluster” objects, that needs to satisfy the following several properties:

1. an entry contains one or more cluster objects at a given numeric location
2. entries are maintained in a numeric key order
3. entries will be frequently inserted and deleted, in arbitrary order
4. given a numeric key value, be able to find the entry nearest to that value
5. given a key, compute a prefix-sum for that value
6. all of the above should be bounded by logarithmic time complexity

Propreties 2,3 and 6 are commonly satisfied by a map structure backed by some variety of balanced tree representation, of which the best-known is the Red-Black tree.

Properties 1, 4 and 5 are more interesting. Property 1 – representing a collection of multiple objects at each entry – can be accomplished in a generalizable way by noting that a collection is representable as a monoid, and so supporting values that can be incremented with respect to a user-supplied monoid relation can satisfy property-1, but also can support many other kinds of update, including but not limited to classical numeric incrementing operations.

Properties 4 and 5 – nearest-entry queries and prefix-sum queries – are also both supportable in logarithmic time using a tree data structure, provided that tree is balanced. Again, the details of the algorithms are out of the current scope, however they are not extremely complex, and their implementations are available in the code.

A reader with their software engineering hat on will notice that these properties are orthogonal. A programmer might be interested in a data structure supporting any one of them, or in some mixed combination. This kind of situation fairly shouts “Scala traits” (or, alternatively, interfaces in Java, etc). With that idea in mind, I designed a system of Scala collection traits that support all of the above properties, in a pure trait form that is fully “mixable” by the programmer, so that one can use exactly the properties needed, but not pay for anything else.

Library Overview

The library consists broadly of 3 kinds of traits:

• tree node traits – implement core tree support for some functionality
• collection traits – provide additional collection API methods the user
• collections – instantiate a usable incarnation of a collection

For the programmer who wishes to either create a trait mixture, or add new mixable traits, the collections also function as reference implementations.

The three tables that follow summarize the currently available traits of each kind listed above. They are (at the time of this posting) all under the package namespace com.redhat.et.silex.maps:

Tree Node Traits

trait	sub-package	description
Node[K]	redblack.tree	Fundamental Red-Black tree functionality
NodeMap[K,V]	ordered.tree	Support a mapping from keys to values
NodeNear[K]	nearest.tree	Nearest-entry query (key-only)
NodeNearMap[K,V]	nearest.tree	Nearest-entry query for key/value maps
NodeInc[K,V]	increment.tree	Increment values w.r.t. a monoid
NodePS[K,V,P]	prefixsum.tree	Prefix sum queries by key (w.r.t. a monoid)

Collection Traits

trait	sub-package	description
OrderedSetLike[K,IN,M]	ordered	ordered set of keys
OrderedMapLike[K,V,IN,M]	ordered	ordered key/value map
NearestSetLike[K,IN,M]	nearest	nearest entry query on keys
NearestMapLike[K,V,IN,M]	nearest	nearest entry query on key/value map
IncrementMapLike[K,V,IN,M]	increment	increment values w.r.t a monoid
PrefixSumMapLike[K,V,P,IN,M]	prefixsum	prefix sum queries w.r.t. a monoid

Concrete Collections

trait	sub-package	description
OrderedSet[K]	ordered	ordered set
OrderedMap[K,V]	ordered	ordered key/value map
NearestSet[K]	nearest	ordered set with nearest-entry query
NearestMap[K,V]	nearest	ordred map with nearest-entry query
IncrementMap[K,V]	increment	ordered map with value increment w.r.t. a monoid
PrefixSumMap[K,V,P]	prefixsum	ordered map with prefix sum query w.r.t. a monoid

The following diagram summarizes the organization and inheritance relationships of the classes.

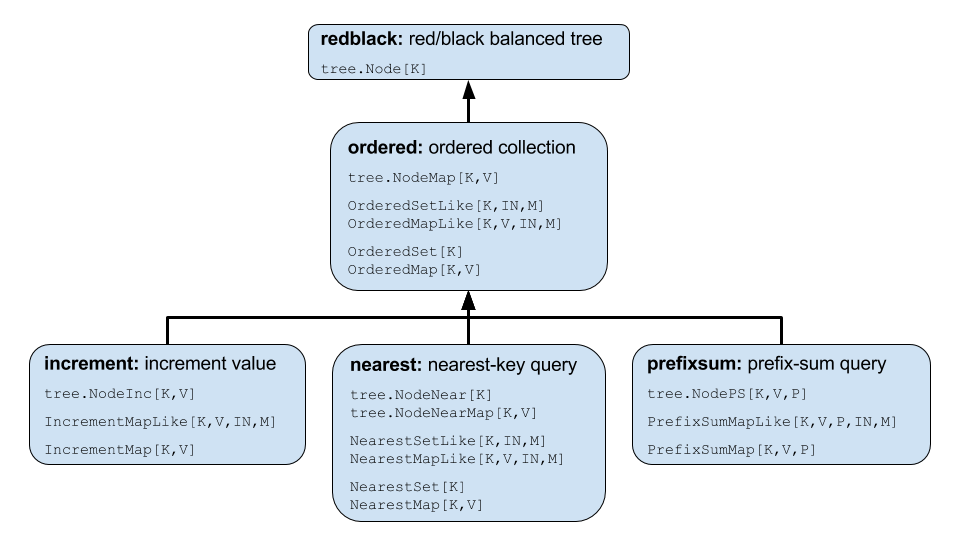
A Red/Black Tree Base Class

The most fundamental trait in this hierarchy is the trait that embodies Red-Black balancing; a “red-black-ness” trait, as it were. This trait supplies the axiomatic tree operations of insertion, deletion and key lookup, where the Red-Black balancing operations are encapsulated for insertion (due to Chris Okasaki) and deletion (due to Stefan Kahrs) Note that Red-Black trees do not assume a separate value, as in a map, but require only keys (thus implementing an ordered set over the key type):

object tree {
  /** The color (red or black) of a node in a Red/Black tree */
  sealed trait Color
  case object R extends Color
  case object B extends Color

  /** Defines the data payload of a tree node */
  trait Data[K] {
    /** The axiomatic unit of data for R/B trees is a key */
    val key: K
  }

  /** Base class of a Red/Black tree node
    * @tparam K The key type
    */
  trait Node[K] {

    /** The ordering that is applied to key values */
    val keyOrdering: Ordering[K]

    /** Instantiate an internal node. */
    protected def iNode(color: Color, d: Data[K], lsub: Node[K], rsub: Node[K]): INode[K]

    // ... declarations for insertion, deletion and key lookup ...

    // ... red-black balancing rules ...
  }
  
   /** Represents a leaf node in the Red Black tree system */
  trait LNode[K] extends Node[K] {
    // ... basis case insertion, deletion, lookup ...
  }

  /** Represents an internal node (Red or Black) in the Red Black tree system */
  trait INode[K] extends Node[K] {
    /** The Red/Black color of this node */
    val color: Color
    /** Including, but not limited to, the key */
    val data: Data[K]
    /** The left sub-tree */
    val lsub: Node[K]
    /** The right sub-tree */
    val rsub: Node[K]

    // ... implementations for insertion, deletion, lookup ...
  }
}

I will assume most readers are familiar with basic binary tree operations, and the Red-Black rules are described elsewhere (I adapted them from the Scala red-black implementation). For the purposes of this discussion, the most interesting feature is that this is a pure Scala trait. All val declarations are abstract. This trait, by itself, cannot function without a subclass to eventually perform dependency injection. However, this abstraction allows the trait to be inherited freely – any programmer can inherit from this trait and get a basic Red-Black balanced tree for (nearly) free, as long as a few basic principles are adhered to for proper dependency injection.

Another detail to call out is the abstraction of the usual key with a Data element. This element represents any node payload that is moved around as a unit during tree structure manipulations, such as balancing pivots. In the case of a map-like subclass, Data is extended to include a value field as well as a key field.

The other noteworthy detail is the abstract definition def iNode(color: Color, d: Data[K], lsub: Node[K], rsub: Node[K]): INode[K] - this is the function called to create any new tree node. In fact, this function, when eventually instantiated, is what performs dependency injection of other tree node fields.

Node Inheritance Example: NodeMap[K,V]

A relatively simple example of node inheritance is hopefully instructive. Here is the definition for tree nodes supporting a key/value map:

object tree {
  /** Trees that back a map-like object have a value as well as a key */
  trait DataMap[K, V] extends Data[K] {
    val value: V
  }

  /** Base class of ordered K/V tree node
    * @tparam K The key type
    * @tparam V The value type
    */
  trait NodeMap[K, V] extends Node[K]

  trait LNodeMap[K, V] extends NodeMap[K, V] with LNode[K]

  trait INodeMap[K, V] extends NodeMap[K, V] with INode[K] {
    val data: DataMap[K, V]
  }
}

Note that in this case very little is added to the red/black functionality already provided by Node[K]. A DataMap[K,V] trait is defined to add a value field in addition to the key, and the internal node INodeMap[K,V] refines the type of its data field to be DataMap[K,V]. The semantics is little more than “tree nodes now carry a value in addition to a key.”

A tree node trait inherits from its own parent class and the corresponding traits for any mixed-in functionality. So for example INodeMap[K,V] inherits from NodeMap[K,V] but also INode[K].

Collection Trait Example: OrderedMapLike[K,V,IN,M]

Continuing with the ordered map example, here is the definition of the collection trait for an ordered map:

trait OrderedMapLike[K, V, IN <: INodeMap[K, V], M <: OrderedMapLike[K, V, IN, M]]
    extends NodeMap[K, V] with OrderedLike[K, IN, M] {

  /** Obtain a new map with a (key, val) pair inserted */
  def +(kv: (K, V)) = this.insert(
    new DataMap[K, V] {
      val key = kv._1
      val value = kv._2
    }).asInstanceOf[M]

  /** Get the value stored at a key, or None if key is not present */
  def get(k: K) = this.getNode(k).map(_.data.value)

  /** Iterator over (key,val) pairs, in key order */
  def iterator = nodesIterator.map(n => ((n.data.key, n.data.value)))

  /** Container of values, in key order */
  def values = valuesIterator.toIterable

  /** Iterator over values, in key order */
  def valuesIterator = nodesIterator.map(_.data.value)
}

You can see that this trait supplies collection API methods that a Scala programmer will recognize as being standard for any map-like collection. Note that this trait also inherits other standard methods from OrderedLike[K,IN,M] (common to both sets and maps) and also inherits from NodeMap[K,V]: In other words, a collection is effectively yet another kind of tree node, with additional collection API methods mixed in. Note also the use of “self types” (the type parameter M), which allows the collection to return objects of its own kind. This is crucial for allowing operations like data insertion to return an object that also supports node insertion, and to maintain consistency of type across operations. The collection type is properly “closed” with respect to its own operations.

Collection Example: OrderedMap[K,V]

To conclude the ordered map example, consider the task of defining a concrete instantiation of an ordered map:

sealed trait OrderedMap[K, V] extends OrderedMapLike[K, V, INodeMap[K, V], OrderedMap[K, V]] {
  override def toString =
    "OrderedMap(" +
      nodesIterator.map(n => s"${n.data.key} -> ${n.data.value}").mkString(", ") +
    ")"
}

You can see that (aside from a convenience override of toString) the trait OrderedMap[K,V] is nothing more than a vehicle for instantiating a particular concrete OrderedMapLike[K,V,IN,M] subtype, with particular concrete types for internal node (INodeMap[K,V]) and its own self-type.

Things become a little more interesting inside the companion object OrderedMap:

object OrderedMap {
  def key[K](implicit ord: Ordering[K]) = new AnyRef {
    def value[V]: OrderedMap[K, V] =
      new InjectMap[K, V](ord) with LNodeMap[K, V] with OrderedMap[K, V]
  }
}

Note that the object returned by the factory method is upcast to OrderedMap[K,V], but in fact has the more complicated type: InjectMap[K,V] with LNodeMap[K,V] with OrderedMap[K,V]. There are a couple things going on here. The trait LNodeMap[K,V] ensures that the new object is in particular a leaf node, which embodies a new empty tree in the Red-Black tree system.

The type InjectMap[K,V] has an even more interesting purpose. Here is its definition:

class InjectMap[K, V](val keyOrdering: Ordering[K]) {
  def iNode(clr: Color, dat: Data[K], ls: Node[K], rs: Node[K]) =
    new InjectMap[K, V](keyOrdering) with INodeMap[K, V] with OrderedMap[K, V] {
      // INode
      val color = clr
      val lsub = ls
      val rsub = rs
      val data = dat.asInstanceOf[DataMap[K, V]]
    }
}

Firstly, note that it is a bona fide class, as opposed to a trait. This class is where, finally, all things abstract are made real – “dependency injection” in the parlance of Scala idioms. You can see that it defines the implementation of abstract method iNode, and that it does this by returning yet another InjectMap[K,V] object, mixed with both INodeMap[K,V] and OrderedMap[K,V], thus maintaining closure with respect to all three slices of functionality: dependency injection, the proper type of internal node, and map collection methods.

The various abstract val fields color, data, lsub and rsub are all given concrete values inside of iNode. Here is where the value of concrete “reference” implementations manifests. Any fields in the relevant internal-node type must be instantiated here, and the logic of instantiation cannot be inherited while still preserving the ability to mix abstract traits. Therefore, any programmer wishing to create a new concrete sub-class must replicate the logic for instantiating all inherited in an internal node.

Another example makes the implications more clear. Here is the definition of injection for a collection that mixes in all three traits for incrementable values, nearest-key queries, and prefix-sum queries:

  class Inject[K, V, P](
    val keyOrdering: Numeric[K],
    val valueMonoid: Monoid[V],
    val prefixMonoid: IncrementingMonoid[P, V]) {
      def iNode(clr: Color, dat: Data[K], ls: Node[K], rs: Node[K]) =
      new Inject[K, V, P](keyOrdering, valueMonoid, prefixMonoid)
          with INodeTD[K, V, P] with TDigestMap[K, V, P] {
        // INode[K]
        val color = clr
        val lsub = ls.asInstanceOf[NodeTD[K, V, P]]
        val rsub = rs.asInstanceOf[NodeTD[K, V, P]]
        val data = dat.asInstanceOf[DataMap[K, V]]
        // INodePS[K, V, P]
        val prefix = prefixMonoid.inc(prefixMonoid.plus(lsub.pfs, rsub.pfs), data.value)
        // INodeNear[K, V]
        val kmin = lsub match {
          case n: INodeTD[K, V, P] => n.kmin
          case _ => data.key
        }
        val kmax = rsub match {
          case n: INodeTD[K, V, P] => n.kmax
          case _ => data.key
        }
      }
  }

Here you can see that all logic for both “basic” internal nodes and also for maintaining prefix sums, and key min/max information for nearest-entry queries, must be supplied. If there is a singularity in this design here is where it is. The saving grace is that it is localized into a single well defined place, and any logic can be transcribed from a proper reference implementation of whatever traits are being mixed.

Finale: Trait Mixing

I will conclude by showing the code for mixing tree node traits and collection traits, which is elegant. Here are type definitions for tree nodes and collection traits that inherit from incrementable values, nearest-key queries, and prefix-sum queries, and there is almost no code except the proper inheritances:

object tree {
  import com.redhat.et.silex.maps.increment.tree._
  import com.redhat.et.silex.maps.prefixsum.tree._
  import com.redhat.et.silex.maps.nearest.tree._

  trait NodeTD[K, V, P] extends NodePS[K, V, P] with NodeInc[K, V] with NodeNearMap[K, V]

  trait LNodeTD[K, V, P] extends NodeTD[K, V, P]
      with LNodePS[K, V, P] with LNodeInc[K, V] with LNodeNearMap[K, V]

  trait INodeTD[K, V, P] extends NodeTD[K, V, P]
      with INodePS[K, V, P] with INodeInc[K, V] with INodeNearMap[K, V] {
    val lsub: NodeTD[K, V, P]
    val rsub: NodeTD[K, V, P]
  }
}

// ...

sealed trait TDigestMap[K, V, P]
  extends IncrementMapLike[K, V, INodeTD[K, V, P], TDigestMap[K, V, P]]
  with PrefixSumMapLike[K, V, P, INodeTD[K, V, P], TDigestMap[K, V, P]]
  with NearestMapLike[K, V, INodeTD[K, V, P], TDigestMap[K, V, P]] {

  override def toString = // ...
}