
 |
Home | Libraries | People | FAQ | More |
#include <boost/math/special_functions/gamma.hpp>
namespace boost{ namespace math{ template <class T1, class T2> calculated-result-type tgamma_ratio(T1 a, T2 b); template <class T1, class T2, class Policy> calculated-result-type tgamma_ratio(T1 a, T2 b, const Policy&); template <class T1, class T2> calculated-result-type tgamma_delta_ratio(T1 a, T2 delta); template <class T1, class T2, class Policy> calculated-result-type tgamma_delta_ratio(T1 a, T2 delta, const Policy&); }} // namespaces
template <class T1, class T2> calculated-result-type tgamma_ratio(T1 a, T2 b); template <class T1, class T2, class Policy> calculated-result-type tgamma_ratio(T1 a, T2 b, const Policy&);
Returns the ratio of gamma functions:
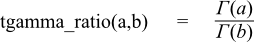
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
Internally this just calls tgamma_delta_ratio(a,
b-a).
template <class T1, class T2> calculated-result-type tgamma_delta_ratio(T1 a, T2 delta); template <class T1, class T2, class Policy> calculated-result-type tgamma_delta_ratio(T1 a, T2 delta, const Policy&);
Returns the ratio of gamma functions:

The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
Note that the result is calculated accurately even when delta is small compared to a: indeed even if a+delta ~ a. The function is typically used when a is large and delta is very small.
The return type of these functions is computed using the result type calculation rules when T1 and T2 are different types, otherwise the result type is simple T1.
The following table shows the peak errors (in units of epsilon) found on various platforms with various floating point types. Unless otherwise specified any floating point type that is narrower than the one shown will have effectively zero error.
Table 3.1. Errors In the Function tgamma_delta_ratio(a, delta)
|
Significand Size |
Platform and Compiler |
20 < a < 80 and delta < 1 |
|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=16.9 Mean=1.7 |
|
64 |
Redhat Linux IA32, gcc-3.4.4 |
Peak=24 Mean=2.7 |
|
64 |
Redhat Linux IA64, gcc-3.4.4 |
Peak=12.8 Mean=1.8 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=21.4 Mean=2.3 |
Table 3.2. Errors In the Function tgamma_ratio(a, b)
|
Significand Size |
Platform and Compiler |
6 < a,b < 50 |
|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=34 Mean=9 |
|
64 |
Redhat Linux IA32, gcc-3.4.4 |
Peak=91 Mean=23 |
|
64 |
Redhat Linux IA64, gcc-3.4.4 |
Peak=35.6 Mean=9.3 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=43.9 Mean=13.2 |
Accuracy tests use data generated at very high precision (with NTL RR class set at 1000-bit precision: about 300 decimal digits) and a deliberately naive calculation of Γ(x)/Γ(y).
The implementation of these functions is very similar to that of beta, and is based on combining similar power terms to improve accuracy and avoid spurious overflow/underflow.
In addition there are optimisations for the situation where delta is a small integer: in which case this function is basically the reciprocal of a rising factorial, or where both arguments are smallish integers: in which case table lookup of factorials can be used to calculate the ratio.