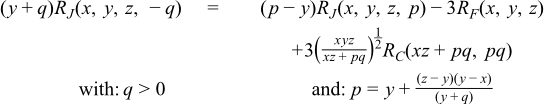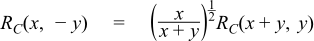|
Home | Libraries | People | FAQ | More |
#include <boost/math/special_functions/ellint_rf.hpp>
namespace boost { namespace math { template <class T1, class T2, class T3> calculated-result-type ellint_rf(T1 x, T2 y, T3 z) template <class T1, class T2, class T3, class Policy> calculated-result-type ellint_rf(T1 x, T2 y, T3 z, const Policy&) }} // namespaces
#include <boost/math/special_functions/ellint_rd.hpp>
namespace boost { namespace math { template <class T1, class T2, class T3> calculated-result-type ellint_rd(T1 x, T2 y, T3 z) template <class T1, class T2, class T3, class Policy> calculated-result-type ellint_rd(T1 x, T2 y, T3 z, const Policy&) }} // namespaces
#include <boost/math/special_functions/ellint_rj.hpp>
namespace boost { namespace math { template <class T1, class T2, class T3, class T4> calculated-result-type ellint_rj(T1 x, T2 y, T3 z, T4 p) template <class T1, class T2, class T3, class T4, class Policy> calculated-result-type ellint_rj(T1 x, T2 y, T3 z, T4 p, const Policy&) }} // namespaces
#include <boost/math/special_functions/ellint_rc.hpp>
namespace boost { namespace math { template <class T1, class T2> calculated-result-type ellint_rc(T1 x, T2 y) template <class T1, class T2, class Policy> calculated-result-type ellint_rc(T1 x, T2 y, const Policy&) }} // namespaces
These functions return Carlson's symmetrical elliptic integrals, the functions have complicated behavior over all their possible domains, but the following graph gives an idea of their behavior:

The return type of these functions is computed using the result type calculation rules when the arguments are of different types: otherwise the return is the same type as the arguments.
template <class T1, class T2, class T3> calculated-result-type ellint_rf(T1 x, T2 y, T3 z) template <class T1, class T2, class T3, class Policy> calculated-result-type ellint_rf(T1 x, T2 y, T3 z, const Policy&)
Returns Carlson's Elliptic Integral RF:

Requires that all of the arguments are non-negative, and at most one may be zero. Otherwise returns the result of domain_error.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
template <class T1, class T2, class T3> calculated-result-type ellint_rd(T1 x, T2 y, T3 z) template <class T1, class T2, class T3, class Policy> calculated-result-type ellint_rd(T1 x, T2 y, T3 z, const Policy&)
Returns Carlson's elliptic integral RD:
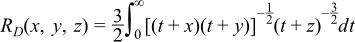
Requires that x and y are non-negative, with at most one of them zero, and that z >= 0. Otherwise returns the result of domain_error.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
template <class T1, class T2, class T3, class T4> calculated-result-type ellint_rj(T1 x, T2 y, T3 z, T4 p) template <class T1, class T2, class T3, class T4, class Policy> calculated-result-type ellint_rj(T1 x, T2 y, T3 z, T4 p, const Policy&)
Returns Carlson's elliptic integral RJ:
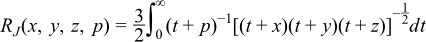
Requires that x, y and z are non-negative, with at most one of them zero, and that p != 0. Otherwise returns the result of domain_error.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
When p < 0 the function returns the Cauchy principal value using the relation:
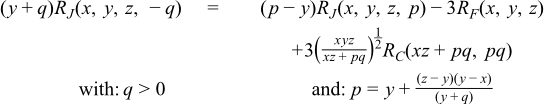
template <class T1, class T2> calculated-result-type ellint_rc(T1 x, T2 y) template <class T1, class T2, class Policy> calculated-result-type ellint_rc(T1 x, T2 y, const Policy&)
Returns Carlson's elliptic integral RC:

Requires that x > 0 and that y != 0. Otherwise returns the result of domain_error.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
When y < 0 the function returns the Cauchy principal value using the relation:
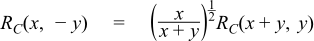
There are two sets of tests.
Spot tests compare selected values with test data given in:
B. C. Carlson, Numerical computation of real or complex elliptic integrals. Numerical Algorithms, Volume 10, Number 1 / March, 1995, pp 13-26.
Random test data generated using NTL::RR at 1000-bit precision and our implementation checks for rounding-errors and/or regressions.
There are also sanity checks that use the inter-relations between the integrals to verify their correctness: see the above Carlson paper for details.
These functions are computed using only basic arithmetic operations, so there isn't much variation in accuracy over differing platforms. Note that only results for the widest floating-point type on the system are given as narrower types have effectively zero error. All values are relative errors in units of epsilon.
Table 3.25. Errors Rates in the Carlson Elliptic Integrals
|
Significand Size |
Platform and Compiler |
RF |
RD |
RJ |
RC |
|---|---|---|---|---|---|
|
53 |
Win32 / Visual C++ 8.0 |
Peak=2.9 Mean=0.75 |
Peak=2.6 Mean=0.9 |
Peak=108 Mean=6.9 |
Peak=2.4 Mean=0.6 |
|
64 |
Red Hat Linux / G++ 3.4 |
Peak=2.5 Mean=0.75 |
Peak=2.7 Mean=0.9 |
Peak=105 Mean=8 |
Peak=1.9 Mean=0.7 |
|
113 |
HP-UX / HP aCC 6 |
Peak=5.3 Mean=1.6 |
Peak=2.9 Mean=0.99 |
Peak=180 Mean=12 |
Peak=1.8 Mean=0.7 |
The key of Carlson's algorithm [Carlson79] is the duplication theorem:
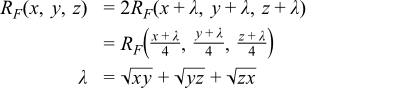
By applying it repeatedly, x, y, z get closer and closer. When they are nearly equal, the special case equation
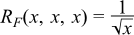
is used. More specifically, [R F] is evaluated from a Taylor series expansion to the fifth order. The calculations of the other three integrals are analogous.
For p < 0 in RJ(x, y, z, p) and y < 0 in RC(x, y), the integrals are singular and their Cauchy principal values are returned via the relations: