Computing Smooth Max and its Gradients Without Over- and Underflow
In my previous post I derived the gradient and Hessian for the smooth max function. The Notorious JDC wrote a helpful companion post that describes computational issues of overflow and underflow with smooth max; values of fk don’t have to grow very large (or small) before floating point limitations start to force their exponentials to +inf or zero. In JDC’s post he discusses this topic in terms of a two-valued smooth max. However it isn’t hard to generalize the idea to a collection of fk. Start by taking the maximum value over our collection of functions, which I’ll define as (z):
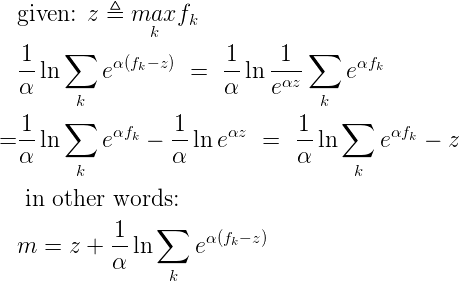
As JDC described in his post, this alternative expression for smooth max (m) is computationally stable. Individual exponential terms may underflow to zero, but they are the ones which are dominated by the other terms, and so approximating them by zero is numerically accurate. In the limit where one value dominates all others, it will be exactly the value given by (z).
It turns out that we can play a similar trick with computing the gradient:
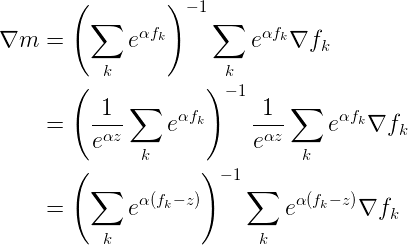
Without showing the derivation, we can apply exactly the same manipulation to the terms of the Hessian:
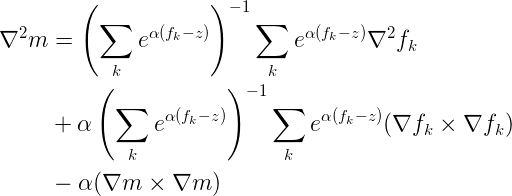
And so we now have a computationally stable form of the equations for smooth max, its gradient and its Hessian. Enjoy!